Machine Learning Homework 5
李姚(LiYao), 117033910023
Problem 1.
(a)
cluster 1: A1 cluster 2: A4, A3, A5, A6, A8 cluster 3: A7, A2
(b)
cluster 1’s center: $(2, 10)$ cluster 2’s center: $(6, 6)$ cluster 3’s center: $(1.5, 3.5)$
(c)
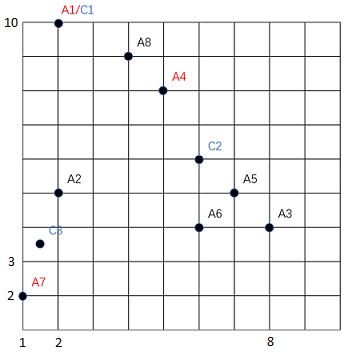
Problem 2.
(a)
\(k(x, x') = \phi(x)^T\phi(x')\)
(b)
Since $HH^T$ is a symmetric matrix, it has the diagonalization form:
\[V^THH^TV = \lambda = \begin{bmatrix} \lambda_1 & \cdots & 0 \\ \ \ \ \ \ \ \ \ \ \ \lambda_2 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \lambda_n \end{bmatrix}\]Thus:
\[\Lambda = H^TV = \begin{bmatrix} \sqrt{\lambda_1} & \cdots & 0 \\ \ \ \ \ \ \ \ \ \ \ \sqrt{\lambda_2} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sqrt{\lambda_n} \end{bmatrix}\]We can see that $\Lambda$ is a diagonal, so it can be transformed from another diagonal matrix:
\[\Lambda = H^THP\]$P$ is the transformation matrix. Then:
\[V = HP\]That is: $V$ is a linear combination of ${\phi(x^1), \phi(x^2), \dots, \phi(x^n)}$
(c)
Let $C = \frac{1}{n} HH^T$, then $CV = \lambda V$.
With $V = \sum_{i}\alpha_i\phi(x^i)$, we have $CV = \frac{1}{n}HH^TH\alpha = \lambda H \alpha$.
Take left multiplication by $H^T$ on both sides,
\[\begin{align} \frac{1}{n}H^THH^TH\alpha &= \lambda H^TH\alpha \\ K^2 \alpha &= n\lambda K \alpha \end{align}\](d)
By utilizing the properties of the kernel function, the PCA can be shown without computing any $\phi(x)$.
(e)
We need the mapping function to map features into higher dimensional spaces. But accually, the mapping function $\phi(x)$ itself is hard to be determined in most cases. The good news is that, without computing $\phi(x)$ explicitly, we can achieve the goal by just computing the inner products throuth the kernel function and the kernel functions are easy-computing most time.
(f)
\(\begin{align}\ \frac{1}{n} K \alpha &= \lambda \alpha \\ K &= {\phi(x)}^T \phi(x) \\ &= \Sigma^T = \Sigma \end{align}\)
Then we take eigen-decomposition on $K$, with $V$ and $\lambda$ being the eigenvector and eigenvalue of $K$.
Problem 3.
E Step: \(\begin{align} P(z_{ik} = 1|x_i, \theta) &= \frac{P(x_i|z_{ik}=1, \theta)P(z_{ik}=1|\theta)}{P(x_i|\theta)} \\ &= \frac{P(x_i|\mu_k)\pi_k}{\sum_{j=1}^{K}P(x_i|\mu_i)\pi_j} \\ &= \frac{\pi_k \Pi_{j=1}^{M}\mu_k(j)^{x_i(j)}}{\sum_{j=1}^{K}\pi_j \Pi_{l=1}^{M}\mu_j(l)^{x_i(l)}} \end{align}\)
M Step: \(\begin{align} P(X, Z|\theta) &= \Pi_{i=1}^{n}P(x_i, z_i|\theta) \\ &= \Pi_{i=1}^{n}P(x_i|z_i,\theta)P(z_i|\theta) \end{align}\)
With: \(\begin{align} P(z_{ik}=1|\theta) &= \pi_k \\ \Rightarrow \ \ P(z_i|\theta) &= \Pi_{k=1}^{K}\pi_k^{z_{jk}} \\ \\ P(x_i|z_{ik}=1,\theta) &= P(x_i|\mu_k) \\ \Rightarrow \ \ P(x_i|z_i,\theta) &= \Pi_{k=1}^{K}P(x_i|\mu_k)^{z_{ik}} \\ &= \Pi_{k=1}^{K}\Pi_{j=1}^{M}[\mu_k(j)^{x_i(j)}]^{z_{ik}} \end{align}\)
Then the likelyhood: \(\begin{align} P(X,Z|\theta) &= \Pi_{i=1}^{n}P(x_i|z_i,\theta)P(z_i|\theta) \\ &= \Pi_{i=1}^{n}\{\Pi_{k=1}^{K}\Pi_{j=1}^{M}[\mu_k(j)^{x_i(j)}]^{z_{ik}}\}[\Pi_{k=1}^{K}\pi_k^{z_{ik}}] \\ &= \Pi_{i=1}^{n}\Pi_{k=1}^{K}[\pi_k \Pi_{j=1}^{M}\mu_k(j)^{x_i(j)}]^{z_{ik}} \end{align}\)
The log likelyhood: \(\begin{align} L(X,Z|\theta) &= ln{P(X,Z|\theta)} \\ &= \sum_{i=1}^{n}\sum_{k=1}^{K}[z_{ik}ln{\pi_k} + z_{ik}\sum_{j=1}^{M}x_i(j)ln{\mu_k(j)}] \end{align}\)
(i) To Estimate $\pi_{kS}$:
Fix $z_{ijS}$ and take the constraint $\sum\pi_k = 1$ Apply Lagrangian multiplier: \(\begin{align} L(\pi_k) &= L(X,Z|\theta) + \lambda(\sum_{l=1}^{K}\pi_l - 1) \\ \frac{\partial{L}}{\partial{\pi_k}} &= \sum_{i=1}^{n}\frac{z_{ik}}{\pi_k} + \lambda = 0 \\ \Rightarrow \ \ \pi_k &= -\frac{1}{\lambda}\sum_{i=1}^{n}z_{ik} \end{align}\)
For the value of $\lambda$, it’s time to utilize the fact $\sum_{l=1}^{K}\pi_l = 1$: \(\begin{align} \sum_{l=1}^{K}\pi_l &= -\frac{1}{\lambda}\sum_{l=1}^{K}\sum_{i=1}^{n}z_{il} = 1 \\ \Rightarrow \ \ -\frac{1}{\lambda} &= \frac{1}{\sum_{l=1}^{K}\sum_{i=1}^{n}z_{il}} \\ \Rightarrow \ \ \pi_k &= \frac{\sum_{i=1}^{n}z_{ik}}{\sum_{l=1}^{K}\sum_{i=1}^{n}z_{il}} = \frac{1}{n}\sum_{i=1}^{n}z_{ik}\\ \end{align}\)
(ii) To Estimate $\mu_{kS}$:
Fix $z_{ijS}$ and take the constraint $\sum_{l}\mu_k(l) = 1$ Apply Lagrangian multiplier: \(\begin{align} L(\mu_k) &= L(X,Z|\theta) + \lambda [\sum_{l=1}^{M}\mu_k(l) - 1] \\ \frac{\partial L}{\partial \mu_k(j)} &= \sum_{i=1}^{n} \frac{z_{ik}x_i(j)}{\mu_k(j)} + \lambda = 0 \\ \end{align}\)
Eliminate $\lambda$ by the same method of utilizing $\sum_{l}\mu_k(l) = 1$, we finally obtain: \(\mu_k(j) = \frac{\sum_{i=1}^{n}z_{ik}x_{ij}}{\sum_{i=1}^{n}z_{ik}}\)